През средата Р на отсечката МN е издигнат перпендикуляр и A e произволна точка от него. Не е вярно твърдението:
Медианата АМ и ъглополовящата СL на Δ АВС са перпендикулярни. Отношението АC : ВС е равно на:
В остроъгълния Δ АВС височините АD и СМ се пресичат в точка Н. Ако АВ = СН и СD = 5 сm, то дължината на АD е:
Височините РА и МВ на остроъгълния Δ МNР се пресичат в точка Н. Ако МN = РН, то мярката на ∠ ВМР е:
За равностранния Δ АВС медианите AQ и CP се пресичат в точка М. Не е вярно твърдението:
За равнобедрения Δ АВС (АС = BС) е построена ъглополовящата АL. Ако ∠ АLВ = 75°, то ъглите на Δ АВС са:
Бедрото на равнобедрен триъгълник е 6 dm, а лицето му е 27 dm2. Точка от основата му е на разстояние 3,6 dm от едното бедро. Разстоянието й до другото бедро е:
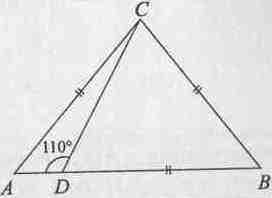
За Δ АВС от чертежа е известно, че АС = ВС = DВ и ∠ ADC = 110°. Градусната мярка на ∠ АСD е:
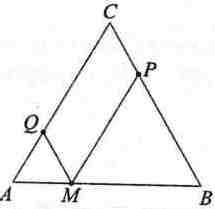
През точка М от основата АВ на равнобедрения Δ АВС са построени прави, успоредни на бедрата, които пресичат АС и ВС съответно в точките Q и Р. Броят на равнобедрените триъгълници е:
Височините АА1 и ВВ1на равнобедрения Δ АВС (АС = СВ) се пресичат в точка Н. Вярно е твърдението:
Еднакви триъгълници. Равнобедрен и равностранен триъгълник
Тестът ви предоставя възможност да проверите знанията си върху: признаци за еднаквост на триъгълници; равнобедрени и равностранни триъгълници; медиана, височина и ъглополовяща в триъгълник.
Информация и рейтинг
| Дата: | 2020-12-08 11:49:20 |
| Предмет: | Математика |
| Предназначен за: | Ученици от 7 клас |
| Въпроси: | 20 въпр. |
| Сподели: |
